求解大型马尔可夫链¶
| 日期 | 2008-12-28(最后修改),2008-12-28(创建) |
|---|
本页展示了如何计算大型马尔可夫链的平稳分布 pi。示例是一个由两个 M/M/1 队列组成的串联系统。通常,马尔可夫链的转移矩阵 P 是稀疏的,因此我们可以使用 scipy.sparse 或 Pysparse。这里我们将演示如何使用这两个工具。
幂法¶
在本节中,我们将通过称为幂法的迭代方法找到 pi。更具体地说,给定一个(随机)转移矩阵 P 和一个初始向量 pi_0,迭代地计算 pi_n = pi_{n-1} P,直到 pi_n 和 pi_{n-1} 之间的距离(在某个范数中)足够小。
首先,我们构建相关马尔可夫链的生成矩阵 Q。然后,我们通过均匀化方法将 Q 转换为转移矩阵 P,即,我们将 P 定义为 I - Q/l,其中 I 是与 Q 相同大小的单位矩阵,l 是 Q 对角线上最小的元素。一旦我们有了 P,我们就可以通过迭代 pi_n = pi_0 P\^n 来近似 pi(满足 pi = pi P 的 P 的左特征向量),其中 pi_0 是某个初始向量。
关于上述方法的更多细节可以在(或多或少)任何关于概率和马尔可夫链的书籍中找到。一个很好的例子,包含许多很好的例子并关注马尔可夫链的数值解,是 G. Bolch 等人撰写的《排队网络与马尔可夫链》,John Wiley,第二版,2006 年。
您可以在此处获取本教程的源代码:tandemqueue.py
在 [ ]
#!/usr/bin/env python
labda, mu1, mu2 = 1., 1.01, 1.001
N1, N2 = 50, 50
size = N1*N2
from numpy import ones, zeros, empty
import scipy.sparse as sp
import pysparse
from pylab import matshow, savefig
from scipy.linalg import norm
import time
这个简单的函数将状态 (i,j) 转换为更适合定义转移矩阵的形式,其中 (i,j) 表示第一个队列包含 i 个作业,第二个队列包含 j 个作业。
在 [ ]
def state(i,j):
return j*N1 + i
构建生成矩阵 Q 的非对角元素。
在 [ ]
def fillOffDiagonal(Q):
# labda
for i in range(0,N1-1):
for j in range(0,N2):
Q[(state(i,j),state(i+1,j))]= labda
# mu2
for i in range(0,N1):
for j in range(1,N2):
Q[(state(i,j),state(i,j-1))]= mu2
# mu1
for i in range(1,N1):
for j in range(0,N2-1):
Q[(state(i,j),state(i-1,j+1))]= mu1
print "ready filling"
在这个函数中,我们使用 scipy.sparse
在 [ ]
def computePiMethod1():
e0 = time.time()
Q = sp.dok_matrix((size,size))
fillOffDiagonal(Q)
# Set the diagonal of Q such that the row sums are zero
Q.setdiag( -Q*ones(size) )
# Compute a suitable stochastic matrix by means of uniformization
l = min(Q.values())*1.001 # avoid periodicity, see the book of Bolch et al.
P = sp.speye(size, size) - Q/l
# compute Pi
P = P.tocsr()
pi = zeros(size); pi1 = zeros(size)
pi[0] = 1;
n = norm(pi - pi1,1); i = 0;
while n > 1e-3 and i < 1e5:
pi1 = pi*P
pi = pi1*P # avoid copying pi1 to pi
n = norm(pi - pi1,1); i += 1
print "Method 1: ", time.time() - e0, i
return pi
现在使用 Pysparse。
在 [ ]
def computePiMethod2():
e0 = time.time()
Q = pysparse.spmatrix.ll_mat(size,size)
fillOffDiagonal(Q)
# fill diagonal
x = empty(size)
Q.matvec(ones(size),x)
Q.put(-x)
# uniformize
l = min(Q.values())*1.001
P = pysparse.spmatrix.ll_mat(size,size)
P.put(ones(size))
P.shift(-1./l, Q)
# Compute pi
P = P.to_csr()
pi = zeros(size); pi1 = zeros(size)
pi[0] = 1;
n = norm(pi - pi1,1); i = 0;
while n > 1e-3 and i < 1e5:
P.matvec_transp(pi,pi1)
P.matvec_transp(pi1,pi)
n = norm(pi - pi1,1); i += 1
print "Method 2: ", time.time() - e0, i
return pi
输出结果。
在 [ ]
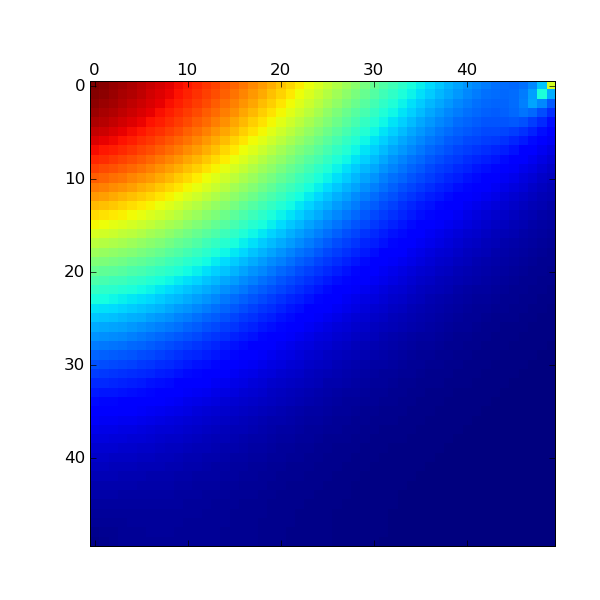
def plotPi(pi):
pi = pi.reshape(N2,N1)
matshow(pi)
savefig("pi.eps")
if __name__ == "__main__":
pi = computePiMethod1()
pi = computePiMethod2()
plotPi(pi)
章节作者:nokfi
附件