眼图

日期2012-02-04 (最后修改), 2012-02-04 (创建)

以下代码生成以下绘图

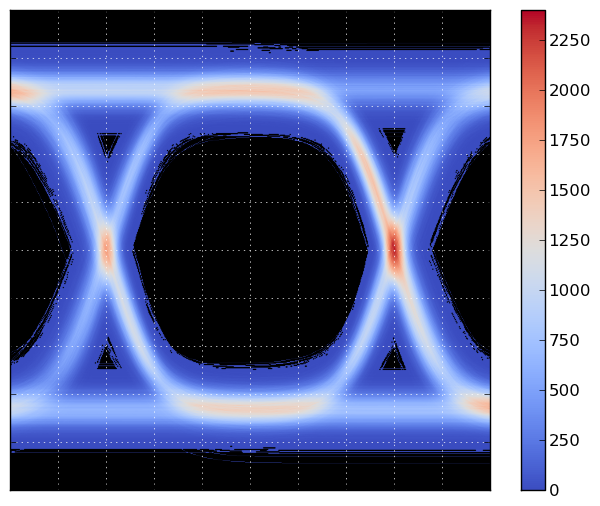
主脚本生成 `num_traces` 条轨迹，并在 600x600 的网格上，计算轨迹穿过网格点的次数。然后使用 matplotlib 的 imshow() 函数绘制网格。计数使用 Bresenham 线算法 执行，以确保计数正确，并且曲线的陡峭部分不会导致计数丢失。

Bresenham 算法在纯 Python 中速度很慢，因此包含了一个 Cython 版本。如果您没有构建 Bresenham 代码的 Cython 版本，请确保在运行程序之前减少 `num_traces`！

以下是主演示脚本 eye_demo.py。

In [2]

#!python
import numpy as np

use_fast = True
try:
    from brescount import bres_curve_count
except ImportError:
    print "The cython version of the curve counter is not available."
    use_fast = False


def bres_segment_count_slow(x0, y0, x1, y1, grid):
    """Bresenham's algorithm.

    The value of grid[x,y] is incremented for each x,y
    in the line from (x0,y0) up to but not including (x1, y1).
    """

    nrows, ncols = grid.shape

    dx = abs(x1 - x0)
    dy = abs(y1 - y0)

    sx = 0
    if x0 < x1:
        sx = 1
    else:
        sx = -1
    sy = 0
    if y0 < y1:
        sy = 1
    else:
        sy = -1

    err = dx - dy

    while True:
        # Note: this test is moved before setting
        # the value, so we don't set the last point.
        if x0 == x1 and y0 == y1:
            break

        if 0 <= x0 < nrows and 0 <= y0 < ncols:
            grid[x0, y0] += 1

        e2 = 2 * err
        if e2 > -dy:
            err -= dy
            x0 += sx
        if e2 < dx:
            err += dx
            y0 += sy

def bres_curve_count_slow(x, y, grid):
    for k in range(x.size - 1):
        x0 = x[k]
        y0 = y[k]
        x1 = x[k+1]
        y1 = y[k+1]
        bres_segment_count_slow(x0, y0, x1, y1, grid)


def random_trace(t):
    s = 2*(np.random.randint(0, 5) % 2) - 1
    r = 0.01 * np.random.randn()
    s += r
    a = 2.0 + 0.001 * np.random.randn()
    q = 2*(np.random.randint(0, 7) % 2) - 1
    t2 = t + q*(6 + 0.01*np.random.randn())
    t2 += 0.05*np.random.randn()*t
    y = a * (np.exp(s*t2) / (1 + np.exp(s*t2)) - 0.5) + 0.07*np.random.randn()
    return y


if __name__ == "__main__":
    import matplotlib.pyplot as plt
    grid_size = 600
    grid = np.zeros((grid_size, grid_size), dtype=np.int32)

    tmin = -10.0
    tmax = 10.0
    n = 81
    t = np.linspace(tmin, tmax, n)
    dt = (tmax - tmin) / (n - 1)

    ymin = -1.5
    ymax = 1.5

    num_traces = 1000

    for k in range(num_traces):

        # Add some noise to the times at which the signal
        # will be sampled.  Without this, all the samples occur
        # at the same times, and this produces an aliasing
        # effect in the resulting bin counts.
        # If n == grid_size, this can be dropped, and t2 = t
        # can be used instead. (Or, implement an antialiased
        # version of bres_curve_count.)
        steps = dt + np.sqrt(0.01 * dt) * np.random.randn(n)
        steps[0] = 0
        steps_sum = steps.cumsum()
        t2 = tmin + (tmax - tmin) * steps_sum / steps_sum[-1]

        td = (((t2 - tmin) / (tmax - tmin)) * grid_size).astype(np.int32)

        y = random_trace(t2)

        # Convert y to integers in the range [0,grid_size).
        yd = (((y - ymin) / (ymax - ymin)) * grid_size).astype(np.int32)

        if use_fast:
            bres_curve_count(td, yd, grid)
        else:
            bres_curve_count_slow(td, yd, grid)

    plt.figure()
    # Convert to float32 so we can use nan instead of 0.
    grid = grid.astype(np.float32)
    grid[grid==0] = np.nan
    plt.grid(color='w')
    plt.imshow(grid.T[::-1,:], extent=[0,1,0,1], cmap=plt.cm.coolwarm,
               interpolation='gaussian')
    ax = plt.gca()
    ax.set_axis_bgcolor('k')
    ax.set_xticks(np.linspace(0,1,11))
    ax.set_yticks(np.linspace(0,1,11))
    ax.set_xticklabels([])
    ax.set_yticklabels([])
    plt.colorbar()
    fig = plt.gcf()

    #plt.savefig("eye-diagram.png", bbox_inches='tight')
    plt.show()

The cython version of the curve counter is not available.

以下是 brescount.pyx，Bresenham 线算法的 Cython 实现

In [ ]

#!python
import numpy as np
cimport numpy as np
cimport cython


@cython.boundscheck(False)
cdef int bres_segment_count(unsigned x0, unsigned y0,
                            unsigned x1, unsigned y1,
                            np.ndarray[np.int32_t, ndim=2] grid):
    """Bresenham's algorithm.

    See http://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm
    """

    cdef unsigned nrows, ncols
    cdef int e2, sx, sy, err
    cdef int dx, dy

    nrows = grid.shape[0]
    ncols = grid.shape[1]

    if x1 > x0:
        dx = x1 - x0
    else:
        dx = x0 - x1
    if y1 > y0:
        dy = y1 - y0
    else:
        dy = y0 - y1

    sx = 0
    if x0 < x1:
        sx = 1
    else:
        sx = -1
    sy = 0
    if y0 < y1:
        sy = 1
    else:
        sy = -1

    err = dx - dy

    while True:
        # Note: this test occurs before increment the
        # grid value, so we don't count the last point.
        if x0 == x1 and y0 == y1:
            break

        if (x0 < nrows) and (y0 < ncols):
            grid[x0, y0] += 1

        e2 = 2 * err
        if e2 > -dy:
            err -= dy
            x0 += sx
        if e2 < dx:
            err += dx
            y0 += sy

    return 0


def bres_curve_count(np.ndarray[np.int32_t, ndim=1] x,
                     np.ndarray[np.int32_t, ndim=1] y,
                     np.ndarray[np.int32_t, ndim=2] grid):
    cdef unsigned k
    cdef int x0, y0, x1, y1

    for k in range(len(x)-1):
        x0 = x[k]
        y0 = y[k]
        x1 = x[k+1]
        y1 = y[k+1]
        bres_segment_count(x0, y0, x1, y1, grid)
    if 0 <= x1 < grid.shape[0] and 0 <= y1 < grid.shape[1]:
        grid[x1, y1] += 1

此文件 setup.py 可用于构建 Cython 扩展模块

In [ ]

#!python
from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext

import numpy

ext = Extension("brescount", ["brescount.pyx"],
    include_dirs = [numpy.get_include()])

setup(ext_modules=[ext],
      cmdclass = {'build_ext': build_ext})

要构建扩展模块，您必须安装 Cython。

您可以按如下方式构建扩展模块

$ python setup.py build_ext --inplace

章节作者：WarrenWeckesser

附件

• eye-diagram3.png