Matplotlib：S 型函数

日期2006-02-09（最后修改），2006-01-22（创建）

matplotlib 绘制函数的方法要求您计算要绘制的曲线的 x 和 y 顶点，然后将其传递给 plot。例如，对于正态 PDF，matplotlib.mlab 提供了这样的函数

In [ ]

from matplotlib.mlab import normpdf
import matplotlib.numerix as nx
import pylab as p

x = nx.arange(-4, 4, 0.01)
y = normpdf(x, 0, 1) # unit normal
p.plot(x,y, color='red', lw=2)
p.show()

当然，有些曲线没有封闭形式的表达式，不适合这种处理。一些 matplotlib 后端具有使用样条曲线（三次和四次）绘制任意路径的功能，但此功能尚未公开给用户（截至 0.83）。如果您需要此功能，请在 邮件列表 上发帖或提交一个 SourceForge 支持请求。

Rich Shepard 对绘制“S 曲线”和“Z 曲线”感兴趣，一些谷歌搜索表明 S 曲线是 sigmoid，而 Z 曲线只是 1.0-sigmoid。sigmoid 有许多简单的形式：例如，Hill 函数、Boltzmann 函数和反正切函数。以下是一个 Boltzmann 函数的示例

In [ ]

import matplotlib.numerix as nx
import pylab as p

def boltzman(x, xmid, tau):
    """
    evaluate the boltzman function with midpoint xmid and time constant tau
    over x
    """
    return 1. / (1. + nx.exp(-(x-xmid)/tau))

x = nx.arange(-6, 6, .01)
S = boltzman(x, 0, 1)
Z = 1-boltzman(x, 0.5, 1)
p.plot(x, S, x, Z, color='red', lw=2)
p.show()

另请参见 mathworld 上的 sigmoid。

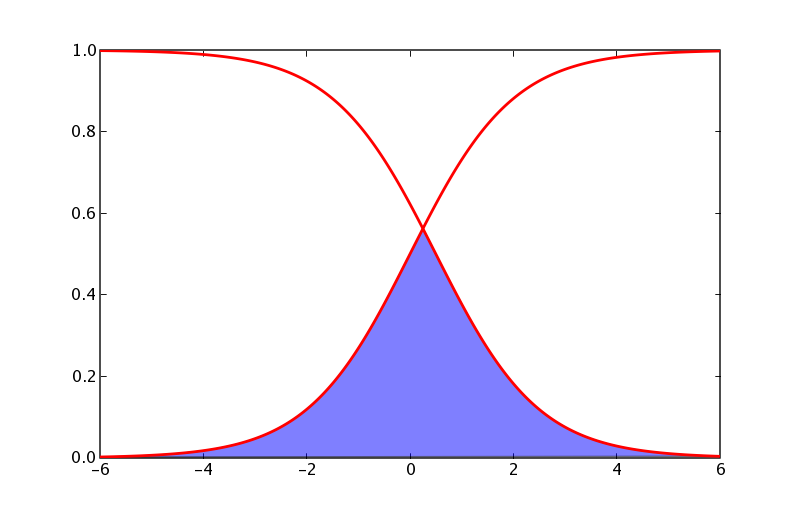
人们通常希望对这些曲线下的区域进行阴影处理，例如 它们交点的下方，您可以使用 numerix 和 matplotlib 的 [http://matplotlib.sourceforge.net/matplotlib.pylab.html#-fill fill] 函数来实现。

In [ ]

import matplotlib.numerix as nx
import pylab as p

def boltzman(x, xmid, tau):
    """
    evaluate the boltzman function with midpoint xmid and time constant tau
    over x
    """
    return 1. / (1. + nx.exp(-(x-xmid)/tau))

def fill_below_intersection(x, S, Z):
    """
    fill the region below the intersection of S and Z
    """
    #find the intersection point
    ind = nx.nonzero( nx.absolute(S-Z)==min(nx.absolute(S-Z)))[0]
    # compute a new curve which we will fill below
    Y = nx.zeros(S.shape, typecode=nx.Float)
    Y[:ind] = S[:ind]  # Y is S up to the intersection
    Y[ind:] = Z[ind:]  # and Z beyond it
    p.fill(x, Y, facecolor='blue', alpha=0.5)

x = nx.arange(-6, 6, .01)
S = boltzman(x, 0, 1)
Z = 1-boltzman(x, 0.5, 1)
p.plot(x, S, x, Z, color='red', lw=2)
fill_below_intersection(x, S, Z)
p.show()

正如这些示例所示，matplotlib 没有提供用于绘制人们想要绘制的所有类型曲线的辅助函数，但它与 numerix 和 python 一起提供了构建这些函数的基本工具。

章节作者：AndrewStraw，RobManagan

附件

• sigmoids.png
• sigmoids2.png