Savitzky Golay 滤波¶
| 日期 | 2012-09-06 (最后修改), 2007-03-06 (创建) |
|---|
Savitzky Golay 滤波器是一种特殊的低通滤波器,非常适合数据平滑。有关更多信息,请参阅:http://www.wire.tu-bs.de/OLDWEB/mameyer/cmr/savgol.pdf (或 http://www.dalkescientific.com/writings/NBN/data/savitzky_golay.py 获取预 numpy 实现)。
示例代码¶
#!python
def savitzky_golay(y, window_size, order, deriv=0, rate=1):
r"""Smooth (and optionally differentiate) data with a Savitzky-Golay filter.
The Savitzky-Golay filter removes high frequency noise from data.
It has the advantage of preserving the original shape and
features of the signal better than other types of filtering
approaches, such as moving averages techniques.
Parameters
----------
y : array_like, shape (N,)
the values of the time history of the signal.
window_size : int
the length of the window. Must be an odd integer number.
order : int
the order of the polynomial used in the filtering.
Must be less then `window_size` - 1.
deriv: int
the order of the derivative to compute (default = 0 means only smoothing)
Returns
-------
ys : ndarray, shape (N)
the smoothed signal (or it's n-th derivative).
Notes
-----
The Savitzky-Golay is a type of low-pass filter, particularly
suited for smoothing noisy data. The main idea behind this
approach is to make for each point a least-square fit with a
polynomial of high order over a odd-sized window centered at
the point.
Examples
--------
t = np.linspace(-4, 4, 500)
y = np.exp( -t**2 ) + np.random.normal(0, 0.05, t.shape)
ysg = savitzky_golay(y, window_size=31, order=4)
import matplotlib.pyplot as plt
plt.plot(t, y, label='Noisy signal')
plt.plot(t, np.exp(-t**2), 'k', lw=1.5, label='Original signal')
plt.plot(t, ysg, 'r', label='Filtered signal')
plt.legend()
plt.show()
References
----------
.. [1] A. Savitzky, M. J. E. Golay, Smoothing and Differentiation of
Data by Simplified Least Squares Procedures. Analytical
Chemistry, 1964, 36 (8), pp 1627-1639.
.. [2] Numerical Recipes 3rd Edition: The Art of Scientific Computing
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery
Cambridge University Press ISBN-13: 9780521880688
"""
import numpy as np
from math import factorial
try:
window_size = np.abs(np.int(window_size))
order = np.abs(np.int(order))
except ValueError, msg:
raise ValueError("window_size and order have to be of type int")
if window_size % 2 != 1 or window_size < 1:
raise TypeError("window_size size must be a positive odd number")
if window_size < order + 2:
raise TypeError("window_size is too small for the polynomials order")
order_range = range(order+1)
half_window = (window_size -1) // 2
# precompute coefficients
b = np.mat([[k**i for i in order_range] for k in range(-half_window, half_window+1)])
m = np.linalg.pinv(b).A[deriv] * rate**deriv * factorial(deriv)
# pad the signal at the extremes with
# values taken from the signal itself
firstvals = y[0] - np.abs( y[1:half_window+1][::-1] - y[0] )
lastvals = y[-1] + np.abs(y[-half_window-1:-1][::-1] - y[-1])
y = np.concatenate((firstvals, y, lastvals))
return np.convolve( m[::-1], y, mode='valid')
代码解释¶
在第 61-62 行,局部最小二乘多项式拟合的系数被预先计算。这些将在后面的第 68 行使用,在那里它们将与信号相关联。为了防止数据极端值出现虚假结果,信号在两端用其镜像填充(第 65-67 行)。
图¶
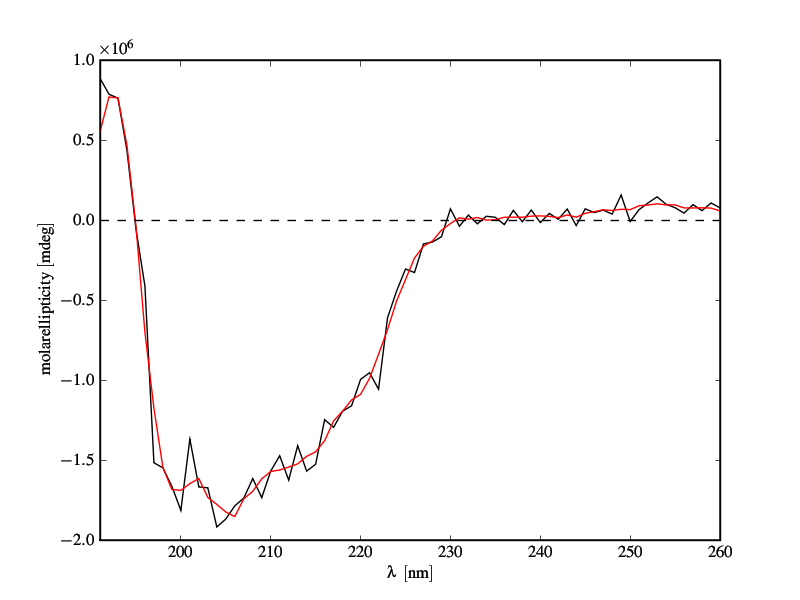
蛋白质的 CD 光谱。黑色:原始数据。红色:应用滤波器
循环伏安法数据的包装器¶
除了平滑 UV-VIS 和 IR 光谱外,S-G 滤波器最流行的应用之一是平滑电分析实验中获得的曲线。在循环伏安法中,电压(作为横坐标)像三角波一样变化。在信号中,在转折点(在切换电位处)存在尖峰,这些尖峰不应该被平滑。在这种情况下,Savitzky-Golay 平滑应该分段进行,即分别对 x 中单调的片段进行平滑。
#!python numbers=disable
def savitzky_golay_piecewise(xvals, data, kernel=11, order =4):
turnpoint=0
last=len(xvals)
if xvals[1]>xvals[0] : #x is increasing?
for i in range(1,last) : #yes
if xvals[i]<xvals[i-1] : #search where x starts to fall
turnpoint=i
break
else: #no, x is decreasing
for i in range(1,last) : #search where it starts to rise
if xvals[i]>xvals[i-1] :
turnpoint=i
break
if turnpoint==0 : #no change in direction of x
return savitzky_golay(data, kernel, order)
else:
#smooth the first piece
firstpart=savitzky_golay(data[0:turnpoint],kernel,order)
#recursively smooth the rest
rest=savitzky_golay_piecewise(xvals[turnpoint:], data[turnpoint:], kernel, order)
return numpy.concatenate((firstpart,rest))
二维数据平滑和最小二乘梯度估计¶
Savitzky-Golay 滤波器也可以用于平滑受噪声影响的二维数据。该算法与一维情况完全相同,只是数学运算稍微复杂一些。基本算法如下:1. 对于二维矩阵的每个点,提取一个子矩阵,以该点为中心,大小等于奇数“窗口大小”。2. 对于此子矩阵,计算一个多项式曲面的最小二乘拟合,定义为 p(x,y) = a0 + a1*x + a2*y + a3*x\^2 + a4*y\^2 + a5*x*y + ... 。请注意,x 和 y 在中心点等于零。3. 用拟合计算的值替换初始中心点。
请注意,由于拟合系数相对于数据间距是线性的,因此可以预先计算以提高效率。此外,重要的是要适当地填充数据的边界,使用数据的镜像,以便在数据的边界处对拟合进行评估可以平滑地进行。
以下是二维滤波的代码。
#!python numbers=enable
def sgolay2d ( z, window_size, order, derivative=None):
"""
"""
# number of terms in the polynomial expression
n_terms = ( order + 1 ) * ( order + 2) / 2.0
if window_size % 2 == 0:
raise ValueError('window_size must be odd')
if window_size**2 < n_terms:
raise ValueError('order is too high for the window size')
half_size = window_size // 2
# exponents of the polynomial.
# p(x,y) = a0 + a1*x + a2*y + a3*x^2 + a4*y^2 + a5*x*y + ...
# this line gives a list of two item tuple. Each tuple contains
# the exponents of the k-th term. First element of tuple is for x
# second element for y.
# Ex. exps = [(0,0), (1,0), (0,1), (2,0), (1,1), (0,2), ...]
exps = [ (k-n, n) for k in range(order+1) for n in range(k+1) ]
# coordinates of points
ind = np.arange(-half_size, half_size+1, dtype=np.float64)
dx = np.repeat( ind, window_size )
dy = np.tile( ind, [window_size, 1]).reshape(window_size**2, )
# build matrix of system of equation
A = np.empty( (window_size**2, len(exps)) )
for i, exp in enumerate( exps ):
A[:,i] = (dx**exp[0]) * (dy**exp[1])
# pad input array with appropriate values at the four borders
new_shape = z.shape[0] + 2*half_size, z.shape[1] + 2*half_size
Z = np.zeros( (new_shape) )
# top band
band = z[0, :]
Z[:half_size, half_size:-half_size] = band - np.abs( np.flipud( z[1:half_size+1, :] ) - band )
# bottom band
band = z[-1, :]
Z[-half_size:, half_size:-half_size] = band + np.abs( np.flipud( z[-half_size-1:-1, :] ) -band )
# left band
band = np.tile( z[:,0].reshape(-1,1), [1,half_size])
Z[half_size:-half_size, :half_size] = band - np.abs( np.fliplr( z[:, 1:half_size+1] ) - band )
# right band
band = np.tile( z[:,-1].reshape(-1,1), [1,half_size] )
Z[half_size:-half_size, -half_size:] = band + np.abs( np.fliplr( z[:, -half_size-1:-1] ) - band )
# central band
Z[half_size:-half_size, half_size:-half_size] = z
# top left corner
band = z[0,0]
Z[:half_size,:half_size] = band - np.abs( np.flipud(np.fliplr(z[1:half_size+1,1:half_size+1]) ) - band )
# bottom right corner
band = z[-1,-1]
Z[-half_size:,-half_size:] = band + np.abs( np.flipud(np.fliplr(z[-half_size-1:-1,-half_size-1:-1]) ) - band )
# top right corner
band = Z[half_size,-half_size:]
Z[:half_size,-half_size:] = band - np.abs( np.flipud(Z[half_size+1:2*half_size+1,-half_size:]) - band )
# bottom left corner
band = Z[-half_size:,half_size].reshape(-1,1)
Z[-half_size:,:half_size] = band - np.abs( np.fliplr(Z[-half_size:, half_size+1:2*half_size+1]) - band )
# solve system and convolve
if derivative == None:
m = np.linalg.pinv(A)[0].reshape((window_size, -1))
return scipy.signal.fftconvolve(Z, m, mode='valid')
elif derivative == 'col':
c = np.linalg.pinv(A)[1].reshape((window_size, -1))
return scipy.signal.fftconvolve(Z, -c, mode='valid')
elif derivative == 'row':
r = np.linalg.pinv(A)[2].reshape((window_size, -1))
return scipy.signal.fftconvolve(Z, -r, mode='valid')
elif derivative == 'both':
c = np.linalg.pinv(A)[1].reshape((window_size, -1))
r = np.linalg.pinv(A)[2].reshape((window_size, -1))
return scipy.signal.fftconvolve(Z, -r, mode='valid'), scipy.signal.fftconvolve(Z, -c, mode='valid')
这是一个演示
#!python number=enable
# create some sample twoD data
x = np.linspace(-3,3,100)
y = np.linspace(-3,3,100)
X, Y = np.meshgrid(x,y)
Z = np.exp( -(X**2+Y**2))
# add noise
Zn = Z + np.random.normal( 0, 0.2, Z.shape )
# filter it
Zf = sgolay2d( Zn, window_size=29, order=4)
# do some plotting
matshow(Z)
matshow(Zn)
matshow(Zf)
附件:Original.pdf 原始数据附件:Original+noise.pdf 原始数据 + 噪声附件:Original+noise+filtered.pdf (原始数据 + 噪声)过滤
二维函数的梯度¶
由于我们已经计算了最佳拟合插值多项式曲面,因此很容易计算其梯度。这种计算二维函数梯度的方法非常稳健,并且部分隐藏了数据中的噪声,而噪声会严重影响微分运算。可以计算的最高阶导数显然取决于拟合中使用的多项式的阶数。
上面提供的代码有一个选项 derivative,它目前允许计算 2D 数据的一阶导数。它可以是“row”或“column”,表示导数的方向,或者“both”,它返回梯度。
章节作者:Unknown[11],Unknown[139],Unknown[140],Unknown[141],WarrenWeckesser,WarrenWeckesser,thomas.haslwanter
附件