应用于薛定谔方程的 FDTD 算法¶
| 日期 | 2008-05-02(最后修改),2007-07-28(创建) |
|---|
以下代码演示了使用一维有限差分时域 (FDTD) 算法来求解简单势的一维薛定谔方程。它只需要 Numpy 和 Matplotlib。
所有数学细节都在此 PDF 中描述:Schrodinger_FDTD.pdf
示例¶
在这些图中,势以任意单位用黄色阴影表示,而波包的总能量以绿色线表示,单位与势相同。因此,虽然能量单位不是左侧轴上的单位,但两个能量图都使用相同的单位,因此可以有效地相互比较。
根据粒子的能量,黄色区域可能是经典禁区(当绿色线位于黄色区域内时)。
波包在 t=0 时开始(显示阶梯势)
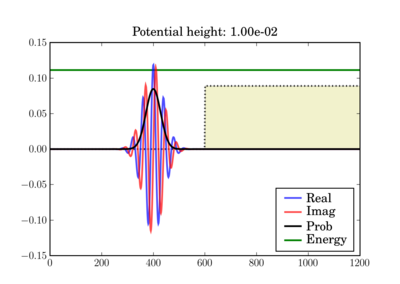
在模拟结束时,它可能看起来像这样,具体取决于实际的势垒高度


这说明了根据势垒高度穿过薄势垒的隧穿。在第二种情况下,经典粒子将完全反弹,因为它的能量低于势垒。
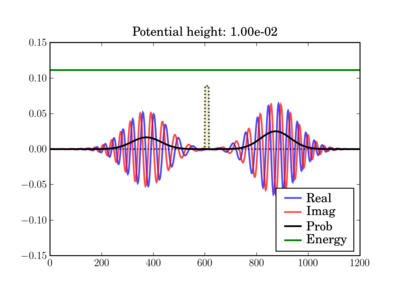
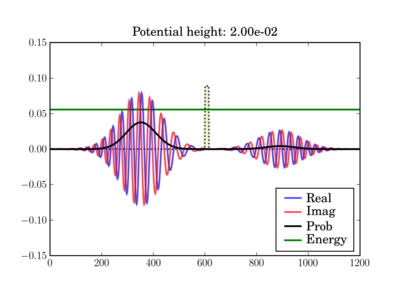
代码¶
在 [1]
#=============================================================================
#
# Quantum Mechanical Simulation using Finite-Difference
# Time-Domain (FDTD) Method
#
# This script simulates a probability wave in the presence of multiple
# potentials. The simulation is c arried out by using the FDTD algorithm
# applied to the Schrodinger equation. The program is intended to act as
# a demonstration of the FDTD algorithm and can be used as an educational
# aid for quantum mechanics and numerical methods. The simulation
# parameters are defined in the code constants and can be freely
# manipulated to see different behaviors.
#
# NOTES
#
# The probability density plots are amplified by a factor for visual
# purposes. The psi_p quanity contains the actual probability density
# without any rescaling.
#
# BEWARE: The time step, dt, has strict requirements or else the
# simulation becomes unstable.
#
# The code has three built-in potential functions for demonstration.
#
# 1) Constant potential: Demonstrates a free particle with dispersion.
#
# 2) Step potential: Demonstrates transmission and reflection.
#
# 3) Potential barrier: Demonstrates tunneling.
#
# By tweaking the height of the potential (V0 below) as well as the
# barrier thickness (THCK below), you can see different behaviors: full
# reflection with no noticeable transmission, transmission and
# reflection, or mostly transmission with tunneling.
#
# This script requires pylab and numpy to be installed with
# Python or else it will not run.
#
#============================================================================
# Author: James Nagel <nagel@mers.byu.edu>
# 5/25/07
#
# Updates by Fernando Perez <Fernando.Perez@colorado.edu>, 7/28/07
#============================================================================
# Numerical and plotting libraries
import numpy as np
import pylab
# Set pylab to interactive mode so plots update when run outside ipython
pylab.ion()
#=============================================================================
# Utility functions
# Defines a quick Gaussian pulse function to act as an envelope to the wave
# function.
def Gaussian(x,t,sigma):
""" A Gaussian curve.
x = Variable
t = time shift
sigma = standard deviation """
return np.exp(-(x-t)**2/(2*sigma**2))
def free(npts):
"Free particle."
return np.zeros(npts)
def step(npts,v0):
"Potential step"
v = free(npts)
v[npts/2:] = v0
return v
def barrier(npts,v0,thickness):
"Barrier potential"
v = free(npts)
v[npts/2:npts/2+thickness] = v0
return v
def fillax(x,y,*args,**kw):
"""Fill the space between an array of y values and the x axis.
All args/kwargs are passed to the pylab.fill function.
Returns the value of the pylab.fill() call.
"""
xx = np.concatenate((x,np.array([x[-1],x[0]],x.dtype)))
yy = np.concatenate((y,np.zeros(2,y.dtype)))
return pylab.fill(xx, yy, *args,**kw)
#=============================================================================
#
# Simulation Constants. Be sure to include decimal points on appropriate
# variables so they become floats instead of integers.
#
N = 1200 # Number of spatial points.
T = 5*N # Number of time steps. 5*N is a nice value for terminating
# before anything reaches the boundaries.
Tp = 50 # Number of time steps to increment before updating the plot.
dx = 1.0e0 # Spatial resolution
m = 1.0e0 # Particle mass
hbar = 1.0e0 # Plank's constant
X = dx*np.linspace(0,N,N) # Spatial axis.
# Potential parameters. By playing with the type of potential and the height
# and thickness (for barriers), you'll see the various transmission/reflection
# regimes of quantum mechanical tunneling.
V0 = 1.0e-2 # Potential amplitude (used for steps and barriers)
THCK = 15 # "Thickness" of the potential barrier (if appropriate
# V-function is chosen)
# Uncomment the potential type you want to use here:
# Zero potential, packet propagates freely.
#POTENTIAL = 'free'
# Potential step. The height (V0) of the potential chosen above will determine
# the amount of reflection/transmission you'll observe
POTENTIAL = 'step'
# Potential barrier. Note that BOTH the potential height (V0) and thickness
# of the barrier (THCK) affect the amount of tunneling vs reflection you'll
# observe.
#POTENTIAL = 'barrier'
# Initial wave function constants
sigma = 40.0 # Standard deviation on the Gaussian envelope (remember Heisenberg
# uncertainty).
x0 = round(N/2) - 5*sigma # Time shift
k0 = np.pi/20 # Wavenumber (note that energy is a function of k)
# Energy for a localized gaussian wavepacket interacting with a localized
# potential (so the interaction term can be neglected by computing the energy
# integral over a region where V=0)
E = (hbar**2/2.0/m)*(k0**2+0.5/sigma**2)
#=============================================================================
# Code begins
#
# You shouldn't need to change anything below unless you want to actually play
# with the numerical algorithm or modify the plotting.
#
# Fill in the appropriate potential function (is there a Python equivalent to
# the SWITCH statement?).
if POTENTIAL=='free':
V = free(N)
elif POTENTIAL=='step':
V = step(N,V0)
elif POTENTIAL=='barrier':
V = barrier(N,V0,THCK)
else:
raise ValueError("Unrecognized potential type: %s" % POTENTIAL)
# More simulation parameters. The maximum stable time step is a function of
# the potential, V.
Vmax = V.max() # Maximum potential of the domain.
dt = hbar/(2*hbar**2/(m*dx**2)+Vmax) # Critical time step.
c1 = hbar*dt/(m*dx**2) # Constant coefficient 1.
c2 = 2*dt/hbar # Constant coefficient 2.
c2V = c2*V # pre-compute outside of update loop
# Print summary info
print 'One-dimensional Schrodinger equation - time evolution'
print 'Wavepacket energy: ',E
print 'Potential type: ',POTENTIAL
print 'Potential height V0: ',V0
print 'Barrier thickness: ',THCK
# Wave functions. Three states represent past, present, and future.
psi_r = np.zeros((3,N)) # Real
psi_i = np.zeros((3,N)) # Imaginary
psi_p = np.zeros(N,) # Observable probability (magnitude-squared
# of the complex wave function).
# Temporal indexing constants, used for accessing rows of the wavefunctions.
PA = 0 # Past
PR = 1 # Present
FU = 2 # Future
# Initialize wave function. A present-only state will "split" with half the
# wave function propagating to the left and the other half to the right.
# Including a "past" state will cause it to propagate one way.
xn = range(1,N/2)
x = X[xn]/dx # Normalized position coordinate
gg = Gaussian(x,x0,sigma)
cx = np.cos(k0*x)
sx = np.sin(k0*x)
psi_r[PR,xn] = cx*gg
psi_i[PR,xn] = sx*gg
psi_r[PA,xn] = cx*gg
psi_i[PA,xn] = sx*gg
# Initial normalization of wavefunctions
# Compute the observable probability.
psi_p = psi_r[PR]**2 + psi_i[PR]**2
# Normalize the wave functions so that the total probability in the simulation
# is equal to 1.
P = dx * psi_p.sum() # Total probability.
nrm = np.sqrt(P)
psi_r /= nrm
psi_i /= nrm
psi_p /= P
# Initialize the figure and axes.
pylab.figure()
xmin = X.min()
xmax = X.max()
ymax = 1.5*(psi_r[PR]).max()
pylab.axis([xmin,xmax,-ymax,ymax])
# Initialize the plots with their own line objects. The figures plot MUCH
# faster if you simply update the lines as opposed to redrawing the entire
# figure. For reference, include the potential function as well.
lineR, = pylab.plot(X,psi_r[PR],'b',alpha=0.7,label='Real')
lineI, = pylab.plot(X,psi_i[PR],'r',alpha=0.7,label='Imag')
lineP, = pylab.plot(X,6*psi_p,'k',label='Prob')
pylab.title('Potential height: %.2e' % V0)
# For non-zero potentials, plot them and shade the classically forbidden region
# in light red, as well as drawing a green line at the wavepacket's total
# energy, in the same units the potential is being plotted.
if Vmax !=0 :
# Scaling factor for energies, so they fit in the same plot as the
# wavefunctions
Efac = ymax/2.0/Vmax
V_plot = V*Efac
pylab.plot(X,V_plot,':k',zorder=0) # Potential line.
fillax(X,V_plot, facecolor='y', alpha=0.2,zorder=0)
# Plot the wavefunction energy, in the same scale as the potential
pylab.axhline(E*Efac,color='g',label='Energy',zorder=1)
pylab.legend(loc='lower right')
pylab.draw()
# I think there's a problem with pylab, because it resets the xlim after
# plotting the E line. Fix it back manually.
pylab.xlim(xmin,xmax)
# Direct index assignment is MUCH faster than using a spatial FOR loop, so
# these constants are used in the update equations. Remember that Python uses
# zero-based indexing.
IDX1 = range(1,N-1) # psi [ k ]
IDX2 = range(2,N) # psi [ k + 1 ]
IDX3 = range(0,N-2) # psi [ k - 1 ]
for t in range(T+1):
# Precompute a couple of indexing constants, this speeds up the computation
psi_rPR = psi_r[PR]
psi_iPR = psi_i[PR]
# Apply the update equations.
psi_i[FU,IDX1] = psi_i[PA,IDX1] + \
c1*(psi_rPR[IDX2] - 2*psi_rPR[IDX1] +
psi_rPR[IDX3])
psi_i[FU] -= c2V*psi_r[PR]
psi_r[FU,IDX1] = psi_r[PA,IDX1] - \
c1*(psi_iPR[IDX2] - 2*psi_iPR[IDX1] +
psi_iPR[IDX3])
psi_r[FU] += c2V*psi_i[PR]
# Increment the time steps. PR -> PA and FU -> PR
psi_r[PA] = psi_rPR
psi_r[PR] = psi_r[FU]
psi_i[PA] = psi_iPR
psi_i[PR] = psi_i[FU]
# Only plot after a few iterations to make the simulation run faster.
if t % Tp == 0:
# Compute observable probability for the plot.
psi_p = psi_r[PR]**2 + psi_i[PR]**2
# Update the plots.
lineR.set_ydata(psi_r[PR])
lineI.set_ydata(psi_i[PR])
# Note: we plot the probability density amplified by a factor so it's a
# bit easier to see.
lineP.set_ydata(6*psi_p)
pylab.draw()
# So the windows don't auto-close at the end if run outside ipython
pylab.ioff()
pylab.show()
部分作者:FernandoPerez、JamesNagel
附件